ARBOL

CONCEPTO

Un arbol es un conjunto finito de 0 o mas nodos v1,v2,...,vn tales que:

1- existe un nodo el cual se distingue de los demas, al mismo lo vamos llamar raiz

2- los demas elementos del conjuntos quedan particionados en m>=0 conjuntos disjuntos T1,T2,...,TN los cuales son arboles.

Los elementos T1,T2,...,TN son llamados subarboles. Vemos aqui la naturaleza recursiva de la estructura arbol, puesto que definimos arbol en termino de arboles. 

TIPOSARBOLES BINARIOS

Un árbol binario es una estructura de datos en la cual cada nodo siempre tiene un hijo izquierdo y un hijo derecho. No pueden tener más de dos hijos (de ahí el nombre "binario"). Si algún hijo tiene como referencia a null, es decir que no almacena ningún dato, entonces este es llamado un nodo externo. En el caso contrario el hijo es llamado un nodo interno. Usos comunes de los árboles binarios son los árboles binarios de búsqueda, los montículos binarios y Codificación de Huffman. 

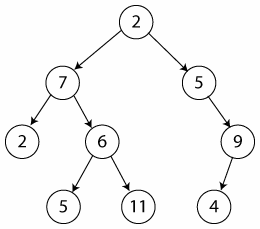
Tipos De Arboles Binarios 
Un árbol binario es un árbol con raíz en el que cada nodo tiene como máximo dos hijos.
Un árbol binario lleno es un árbol en el que cada nodo tiene cero o dos hijos.
Un árbol binario perfecto es un árbol binario lleno en el que todas las hojas (vértices con cero hijos) están a la misma profundidad (distancia desde la raíz, también llamada altura).
A veces un árbol binario perfecto es denominado árbol binario completo. Otros definen un árbol binario completo como un árbol binario lleno en el que todas las hojas están a profundidad n o n-1, para alguna n.Un árbol binario es un árbol en el que ningún nodo puede tener más de dos subárboles. En un árbol binario cada nodo puede tener cero, uno o dos hijos (subárboles). Se conoce el nodo de la izquierda como hijo izquierdo y el nodo de la derecha como hijo derecho. 
ARBOL BINARIO DE BUSQUEDA AUTO-BALANCEABLEUn árbol binario de búsqueda auto-balanceable o equilibrado es un árbol binario de búsqueda que intenta mantener su altura, o el número de niveles de nodos bajo la raíz, tan pequeños como sea posible en todo momento, automáticamente. Esto es importante, ya que muchas operaciones en un árbol de búsqueda binaria tardan un tiempo proporcional a la altura del árbol, y los árboles binarios de búsqueda ordinarios pueden tomar alturas muy grandes en situaciones normales, como cuando las claves son insertadas en orden. Mantener baja la altura se consigue habitualmente realizando transformaciones en el árbol, como la rotación de árboles, en momentos clave. 


RECORRIDOS

PREORDEN

Sea T un arbol ordenado con raız r . Si T consta solo de r , entonces r es el recorrido preorden de T. Sino, suponga que T1, T2, . . . , Tn son los subarboles en r listados de izquierda a derecha en T. El recorrido en preorden inicia visitando r , continua recorriendo T1 en preorden, luego T2, en preorden, y ası sucesivamente hasta recorrer Tn en preorden. 

Procedimiento Preorden ( T: arbol ordenado con raiz)
r = raiz de T
mostrar (r )
Para cada hijo c de r de izquierda a derecha
T(c) = subarbol con c como su raiz
Preorden(T(c))
Fin Para
Fin Procedimiento 
INORDEN 
Sea T un arbol ordenado con raız r . Si T consta solo de r , entonces r es el recorrido en inorden de T. Sino, suponga que T1, T2, . . . , Tn son los subarboles en r listados de izquierda a derecha en T. El recorrido en inorden inicia recorriendo T1 en inorden y continua visitando r , a continuacion recorre T2 en inorden, luego T3, en inorden, y asi sucesivamente hasta recorer Tn en inorden. 
Procedimiento Inorden ( T: arbol ordenado con raiz)
r = raiz de T
Si r es una hoja
mostrar (r )
Sino
l = primer hijo de r de izquierda a derecha
T(l) = subarbol de raiz l
Inorden (T(l))
mostrar (T(l))
Para cada hijo c de r excepto para l y
de izquierda a derecha
T(c) = subarbol de raiz c
Inorden(T(c))
Fin Para
Fin Si
Fin Procedimiento 
POSTORDEN 
Sea T un arbol ordenado con raız r . Si T consta solo de r , entonces r es el recorrido en postorden de T. Sino, suponga que T1, T2, . . . , Tn son los subarboles en r listados de izquierda a derecha en T. El recorrido en postorden inicia recorriendo T1 en postorden, luego recorre T2 en postorden y ası sucesivamente hasta recorrer Tn en postorden y finaliza visitando r . 

Procedimiento Postorden ( T: arbol ordenado con raiz )
r = raiz de T
Para cada hijo c de r de izquierda a derecha
T(c) = subarbol de raiz c
Postorden(T(c))
Fin Para
mostrar (r )
Fin Procedimiento 
ARBOL GENEALOGICO 
BOSQUES 

Un bosque es un conjunto de n ≥ 0 árboles disjuntos. El concepto de bosque esta fuertemente relacionado al de árbol ya que si removemos la raíz de un árbol obtenemos un bosque.