GRAFOS

CONCEPTO

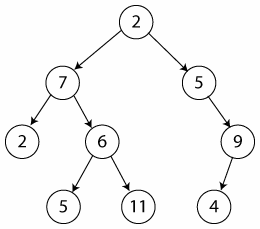
La teoría de grafos (también llamada teoría de las gráficas) estudia las propiedades de los grafos (también llamadas gráficas). Un grafo es un conjunto, no vacío, de objetos llamados vértices (o nodos) y una selección de pares de vértices, llamados aristas (edges en inglés) que pueden ser orientados o no. 

Típicamente, un grafo se representa mediante una serie de puntos (los vértices) conectados por líneas (las aristas). 



TIPOS


NO DIRIGIDOS 

Son aquellos en los cuales los lados no están orientados (No son flechas). Cada lado se representa entre paréntesis, separando sus vértices por comas, y teniendo en cuenta (Vi,Vj)=(Vj,Vi). 

DIRIGIDOS 

Son aquellos en los cuales los lados están orientados (flechas). Cada lado se representa entre ángulos, separando sus vértices por comas y teniendo en cuenta <Vi ,Vj>!=<Vj ,Vi>. En grafos dirigidos, para cada lado <A,B>, A, el cual es el vértice origen, se conoce como la cola del lado y B, el cual es el vértice destino, se conoce como cabeza del lado. 

VERTICES 

Un vértice o nodo es la unidad fundamental de la que están formados los grafos. Los vértices son tratados como objetos indivisibles y sin propiedades, aunque puedan tener una estructura adicional dependiendo de la aplicación por la cual se usa el grafo; por ejemplo, una red semántica es un grafo en donde los vértices representan conceptos o clases de objetos. 

ARCO 

El arco es la union que se se tiene entre dos vertices, cada arco se representa a traves de un par, donde cada elemento determina uno de los vertices. 

CAMINOS 

Un camino en un grafo es una sucesión finita en la que aparecen alternadamente vértices y aristas de dicho grafo. Otras definiciones básicas son:

Los extremos son los vértices inicial y final del camino.

La longitud de un camino es el numero de aristas que contiene.

Un camino es cerrado si sus extremos coinciden.

Un camino es simple si en la sucesión de vértices no hay ninguno repetido.

Un ciclo es un camino cerrado donde los únicos vértices repetidos son el primero y el ultimo.

Un circuito es un camino cerrado que no repite aristas.

Si en un grafo existe un camino que conecta dos vértices distintos, entonces existe un camino simple con extremos en dichos vértices.

Un grafo es conexo si para cada par de vértices, existe un camino con extremos en dichos vértices.

Tipos de caminos

Camino euleriano:

es un camino o circuito que contiene todas las aristas apareciendo cada una de ellas exactamente una vez. Un grafo que admite dicho circuito se denomina grafo euleriano, y sus vértices o tienen grado par o dos de los vértices tienen grado impar.

Camino hamiltoniano:

es un camino simple que contiene todos los vértices apareciendo cada uno de ellos exactamente una vez. Un ciclo que a su vez es un camino hamiltoniano se denomina ciclo hamiltoniano, y un grafo que contiene un ciclo hamiltoniano se denomina grafo hamiltoniano.

ARBOL

CONCEPTO

Un arbol es un conjunto finito de 0 o mas nodos v1,v2,...,vn tales que:

1- existe un nodo el cual se distingue de los demas, al mismo lo vamos llamar raiz

2- los demas elementos del conjuntos quedan particionados en m>=0 conjuntos disjuntos T1,T2,...,TN los cuales son arboles.

Los elementos T1,T2,...,TN son llamados subarboles. Vemos aqui la naturaleza recursiva de la estructura arbol, puesto que definimos arbol en termino de arboles. 

TIPOSARBOLES BINARIOS

Un árbol binario es una estructura de datos en la cual cada nodo siempre tiene un hijo izquierdo y un hijo derecho. No pueden tener más de dos hijos (de ahí el nombre "binario"). Si algún hijo tiene como referencia a null, es decir que no almacena ningún dato, entonces este es llamado un nodo externo. En el caso contrario el hijo es llamado un nodo interno. Usos comunes de los árboles binarios son los árboles binarios de búsqueda, los montículos binarios y Codificación de Huffman. 

Tipos De Arboles Binarios 
Un árbol binario es un árbol con raíz en el que cada nodo tiene como máximo dos hijos.
Un árbol binario lleno es un árbol en el que cada nodo tiene cero o dos hijos.
Un árbol binario perfecto es un árbol binario lleno en el que todas las hojas (vértices con cero hijos) están a la misma profundidad (distancia desde la raíz, también llamada altura).
A veces un árbol binario perfecto es denominado árbol binario completo. Otros definen un árbol binario completo como un árbol binario lleno en el que todas las hojas están a profundidad n o n-1, para alguna n.Un árbol binario es un árbol en el que ningún nodo puede tener más de dos subárboles. En un árbol binario cada nodo puede tener cero, uno o dos hijos (subárboles). Se conoce el nodo de la izquierda como hijo izquierdo y el nodo de la derecha como hijo derecho. 
ARBOL BINARIO DE BUSQUEDA AUTO-BALANCEABLEUn árbol binario de búsqueda auto-balanceable o equilibrado es un árbol binario de búsqueda que intenta mantener su altura, o el número de niveles de nodos bajo la raíz, tan pequeños como sea posible en todo momento, automáticamente. Esto es importante, ya que muchas operaciones en un árbol de búsqueda binaria tardan un tiempo proporcional a la altura del árbol, y los árboles binarios de búsqueda ordinarios pueden tomar alturas muy grandes en situaciones normales, como cuando las claves son insertadas en orden. Mantener baja la altura se consigue habitualmente realizando transformaciones en el árbol, como la rotación de árboles, en momentos clave. 


RECORRIDOS

PREORDEN

Sea T un arbol ordenado con raız r . Si T consta solo de r , entonces r es el recorrido preorden de T. Sino, suponga que T1, T2, . . . , Tn son los subarboles en r listados de izquierda a derecha en T. El recorrido en preorden inicia visitando r , continua recorriendo T1 en preorden, luego T2, en preorden, y ası sucesivamente hasta recorrer Tn en preorden. 

Procedimiento Preorden ( T: arbol ordenado con raiz)
r = raiz de T
mostrar (r )
Para cada hijo c de r de izquierda a derecha
T(c) = subarbol con c como su raiz
Preorden(T(c))
Fin Para
Fin Procedimiento 
INORDEN 
Sea T un arbol ordenado con raız r . Si T consta solo de r , entonces r es el recorrido en inorden de T. Sino, suponga que T1, T2, . . . , Tn son los subarboles en r listados de izquierda a derecha en T. El recorrido en inorden inicia recorriendo T1 en inorden y continua visitando r , a continuacion recorre T2 en inorden, luego T3, en inorden, y asi sucesivamente hasta recorer Tn en inorden. 
Procedimiento Inorden ( T: arbol ordenado con raiz)
r = raiz de T
Si r es una hoja
mostrar (r )
Sino
l = primer hijo de r de izquierda a derecha
T(l) = subarbol de raiz l
Inorden (T(l))
mostrar (T(l))
Para cada hijo c de r excepto para l y
de izquierda a derecha
T(c) = subarbol de raiz c
Inorden(T(c))
Fin Para
Fin Si
Fin Procedimiento 
POSTORDEN 
Sea T un arbol ordenado con raız r . Si T consta solo de r , entonces r es el recorrido en postorden de T. Sino, suponga que T1, T2, . . . , Tn son los subarboles en r listados de izquierda a derecha en T. El recorrido en postorden inicia recorriendo T1 en postorden, luego recorre T2 en postorden y ası sucesivamente hasta recorrer Tn en postorden y finaliza visitando r . 

Procedimiento Postorden ( T: arbol ordenado con raiz )
r = raiz de T
Para cada hijo c de r de izquierda a derecha
T(c) = subarbol de raiz c
Postorden(T(c))
Fin Para
mostrar (r )
Fin Procedimiento 
ARBOL GENEALOGICO 
BOSQUES 

Un bosque es un conjunto de n ≥ 0 árboles disjuntos. El concepto de bosque esta fuertemente relacionado al de árbol ya que si removemos la raíz de un árbol obtenemos un bosque. 

LISTAS

Consiste en una secuencia de nodos, en los que se guardan campos de datos arbitrarios y una o dos referencias, enlaces o punteros (punteros) al nodo anterior o posterior.



Listas simples enlazadas
La lista enlazada básica es la lista enlazada simple la cual tiene un enlace por nodo. Este enlace apunta al siguiente nodo en la lista, o al valor NULL o a la lista vacía, si es el último nodo.
[editar]


Lista Doblemente Enlazada
Un tipo de lista enlazada más sofisticado es la lista doblemente enlazada o lista enlazadas de dos vías. Cada nodo tiene dos enlaces: uno apunta al nodo anterior, o apunta al valor NULL si es el primer nodo; y otro que apunta al nodo siguiente, o apunta al valor NULL si es el último nodo.

Listas enlazadas circulares

En una lista enlazada circular, el primer y el último nodo están unidos juntos. Esto se puede hacer tanto para listas enlazadas simples como para las doblemente enlazadas. Para recorrer una lista enlazada circular podemos empezar por cualquier nodo y seguir la lista en cualquier dirección hasta que se regrese hasta el nodo original.

 

LISTA A PILA

(PILA DINAMICA)

package listaligada;

import java.util.ArrayList;

import java.util.Iterator;

import java.util.LinkedList;

import java.util.List;

import java.util.Scanner;

/**

 *

 * @author PC135-23

 */

public class ListaLigada {

    public static void main (String args[]) {

                    Scanner leer = new Scanner(System.in);

                    int num;

                    int op;

                    LinkedList lista = new LinkedList();

                    do{

                        System.out.println( "\t Menú \t" );

                        System.out.println( "Operaciones con listas" );

                        System.out.println( "1.- Insertar al principio" );

                         System.out.println( "2.- Insertar siguiente" );

                        System.out.println( "3.- Borrar al final" );

                        System.out.println( "4.- Mostrar la lista" );

                        System.out.println( "5.- Borrar toda la lista" );

                        System.out.println( "6.- Salir" );

                        System.out.println( "\n" );

                        System.out.println( "Elija la operación que desee" );

 op = leer.nextInt();

 switch(op){

 case 1:

       System.out.println( "Inserte numero" );

        num = leer.nextInt();

        lista.addFirst(num);

        break;

case 2:

        System.out.println( "Inserte numero" );

         num = leer.nextInt();

         lista.addLast(num);

         break;

case 3:

           System.out.println( "Se borrara el nodo final" );

            lista.removeLast();

            break;

 case 4:

       System.out.println( "La lista es la siguiente" );

       List lista2 = new ArrayList(lista);

       Iterator it = lista2.iterator();

        while (it.hasNext()){

         System.out.println(it.next()+"");

          }

          break;

            case 5:

                 System.out.println( "Se borraran todos los elementos de la lista" );

                 lista.clear();

                 break;

                  case 6:

                     System.out.println( "Al rato" );

                      break;

                       }

                        }

while( op != 7 );

                }

            }

LISTA A COLA

package listaligada;

import java.util.ArrayList;

import java.util.Iterator;

import java.util.LinkedList;

import java.util.List;

import java.util.Scanner;

/**

 *

 * @author PC135-23

 */

public class ListaLigada {

        public static void main (String args[]) {

                    Scanner leer = new Scanner(System.in);

                    int num;

                    int op;

                    LinkedList lista = new LinkedList();

                    do{

                        System.out.println( "\t Menú \t" );

                        System.out.println( "Operaciones con listas" );

                        System.out.println( "1.- Insertar al principio" );

                         System.out.println( "2.- Insertar siguiente" );

                        System.out.println( "3.- Borrar el principio" );

                        System.out.println( "4.- Mostrar la lista" );

                        System.out.println( "5.- Borrar toda la lista" );

                        System.out.println( "6.- Salir" );

                        System.out.println( "\n" );

                        System.out.println( "Elija la operación que desee" );

 op = leer.nextInt();

 switch(op){

 case 1:

       System.out.println( "Inserte numero" );

        num = leer.nextInt();

        lista.addFirst(num);

        break;

case 2:

        System.out.println( "Inserte numero" );

         num = leer.nextInt();

         lista.addLast(num);

         break;

case 3:

           System.out.println( "Se borrara el nodo del principio" );

            lista.removeFirst();

            break;

 case 4:

       System.out.println( "La lista es la siguiente" );

       List lista2 = new ArrayList(lista);

       Iterator it = lista2.iterator();

        while (it.hasNext()){

         System.out.println(it.next()+"");

          }

          break;

            case 5:

                 System.out.println( "Se borraran todos los elementos de la lista" );

                 lista.clear();

                 break;

                  case 6:

                     System.out.println( "Al rato" );

                      break;

                       }

                        }

while( op != 7 );

                }

            }

COLAS

es simplemente un lugar para almacenar cosas, donde esas cosas se insertan una detrás de otra y para extraer siempre se lo hace por adelante de la cola donde se encuentra el primer elemento. Una cola funciona como una fila o cola de personas, que esperan su turno para ser atendidas, la primera persona atendida es siempre la primera de la fila y cuando llega una persona y queremos incorporarla a cola o adicionarla debemos hacerlo por detrás de la ultima persona en la cola.

Con fines educativos una cola se la puede representar gráficamente así:

n	retorna verdad si es que la cola esta llena, pasa cuando se ha llenado todo el vector, la cantidad de elemento que permite la cola lo determina la variable MAXIMO.
adicionar(int a)	adiciona un nuevo elemento a la cola, para esto solo se incrementa la variable fin y se coloca el elemento en esa posición.
eliminar() : int	extrae el primer elemento de la cola, para esto se retorna la posición inicio + 1 del vector y se incrementa inicioen 1.
tamanio() : int	retorna la cantidad de elementos que tiene la cola, para realizar esto se realiza la resta fin - inicio.
copiar(Cola B)	copia tal cual la cola B a la cola destino, al finalizar cola B queda totalmente vacía. Este método es muy útil al momento de hacer operaciones con colas.

ejemplo:

package cola;

/**

 *

 * @author PC-135-23

 */

import java.util.Scanner; 

public class colas { 

 public static void main(String[]args){

          int dato; 

          int inicio; 

          int cola[]=new int[5]; 

           Scanner teclado=new Scanner(System.in);

           for(int fin=0;fin<=5;fin++){ 

                System.out.println("Proporciona datos para la cola"); 

        dato=teclado.nextInt(); 

        cola[fin]=dato; 

         } 

    for(int fin=0;fin>=5;fin--)

        System.out.println("La cola tiene los siguientes datos:"+cola[fin]); 

    } 

}

PILAS

En palabras sencillas es un lugar donde se almacenan datos, al igual que en un Array, pero una Pila tiene una filosofía de entrada y salida de datos, esta filosofía es la LIFO (Last In First Out, en español, ultimo en entrar, primero en salir). 

 

 Los métodos principales de una Pila son:

esVacia()	retorna verdad o falso si la Pila esta vacía, es decir que no tiene ningún elemento, retorna unboolean.
apilar(int a)	adiciona el elemento a en la Pila.
desapilar()	elimina el elemento de la cima de la pila.
vaciar(Pila B)	vacía todo el contenido de la Pila B en la Pila, dejando a B vacía.
tamanio()	retorna cuantos elementos tenemos en la Pila.
cima()	retorna el elemento de la cima sin eliminarlo de la Pila.
mostrar()	muestra todos los elementos de la Pila en modo Consola.

Siguiendo la filosofía se adicionar elementos apilando uno debajo de otro.


Para eliminar un elemento, se extrae o desapila un elemento por la cima.


Otro método que necesita explicación es el método vaciar, un método muy útil que también utilizamos para mostrar la Pila es el vaciar.


Luego la Pila principal queda vacía y la pila B queda así:

ejemplo de pila:

package pila

/**

 *

 * @author PC-135-23

 */

import java.util.Scanner;

public class PilaEstatica { 

public static void main(String[]args){

    int dato;  

    int pila[]=new int[5];  

     Scanner teclado=new Scanner(System.in);

    for(int tope=0;tope<=4;tope++){  

        System.out.println("Proporciona datos para la pila"); 

        dato=teclado.nextInt(); 

        pila[tope]=dato; 

    } 

    for(int tope=4;tope>=0;tope--)

        System.out.println("La pila tiene los siguientes datos:"+pila[tope]);

    } 

} 

MATRICES

DEFINICION DE UNA MATRIZ

La definicion de una matriz numerica multidimensional se hace de esta forma:


tipo[][]...nombrematriz=new|tipo[s1][s2]...


Tipo no es mas que el tipo de elementos (enteros, reales...)


El numero de elementos de la matriz biene dado por el producto de s1 por s2 (s1 filas, s2 columnas)


Un ejemplo concreto:


int[][]m=new int[2][7]




ejemplos de la clase



package matrizunidadapp;

/**

*

* @author PC135-23

*/

public class MatrizUnidadApp {

public static void main (String[] args) {

double[][] mUnidad= new double[4][4];

for (int i=0; i < mUnidad.length; i++) {

for (int j=0; j < mUnidad[i].length; j++) {

if (i == j) {

mUnidad[i][j]=1.0;

}else {

mUnidad[i][j] = 0.0;

}

}

}

for (int i=0; i < mUnidad.length; i++) {

for (int j=0; j < mUnidad[i].length; j++) {

System.out.print(mUnidad[i][j]+"\t");

}

System.out.println("");

}

}

}



otro ejemplo de la clase



package matrizcalif;

import java.util.Scanner;

/**

*

* @author PC135-23

*/

public class MatrizCalif {

public static void main (String args []) {

int i,j;

double suma, promedio,parcial;

double calif [][]=new double[22][5];

Scanner captura= new Scanner(System.in);

for(i=0; i<22; i++)//las filas

{

suma=0;

System.out.println("Ingrese las calificaciones:");

for(j=0; j<5; j++)//columnas

{

parcial=captura.nextDouble();

calif[i][j]=parcial;

suma=suma+calif[i][j];

}

promedio=suma/5;

System.out.println( "El alumno, tiene un promedio de: "+promedio);

}

}

}

Programa que genera una matriz de dos dimensiones con letras del alfabeto, mostrándola posteriormente en pantalla. 01.public static void main(String[] args) { 02.final int FILAS = 3; 03.final int COLUMNAS = 5; 04.char letras[][] = new char[FILAS][COLUMNAS]; 05.char letraQueToca = 'A'; 06.  07.//Carga las letras en la matriz 08.for(int f=0; f<FILAS; f++) { 09.for(int c=0; c<COLUMNAS; c++) { 10.letras[f][c] = letraQueToca; 11.letraQueToca++; 12.} 13.} 14.  15.//Mostrar en pantalla la matriz 16.for(int f=0; f<FILAS; f++) { 17.for(int c=0; c<COLUMNAS; c++) { 18.System.out.print(letras[f][c]+" "); 19.} 20.System.out.println(); 21.} 22.} Programa que genera una matriz representando un triángulo invertido alineado a la derecha realizado con asteriscos, cuyo tamaño será especificado por el usuario. La matriz será mostrada en pantalla finalmente. Por ejemplo, si se indica el tamaño 5 deberá aparecer: *****  ****   ***    **     * 01.public static void main(String[] args) { 02.final int TAM = 5; 03.char triangulo[][] = new char[TAM][TAM]; 04.  05.//Cargar matriz con el dibujo 06.for(int f=0; f<TAM; f++) { 07.//Bucle para mostrar espacios 08.for(int c=0; c<f; c++) 09.triangulo[f][c] = ' '; 10.//Bucle para mostrar asteriscos 11.for(int c=f; c<TAM; c++) 12.triangulo[f][c] = '*'; 13.} 14.  15.//Mostrar matriz en pantalla 16.for(int f=0; f<TAM; f++) { 17.for(int c=0; c<TAM; c++) 18.System.out.print(triangulo[f][c]); 19.System.out.println(); 20.} 21.}